unidad 3
UNIVERSIDAD AUTÓNOMA DE GUERRERO
UNIDAD ACADÉMICA DE INGENIERA
UNIDAD DE APRENDIZAJE: MÉTODOS NUMÉRICOS
TEMA :
BLOGGER DE COMPETENCIA # 3
NOMBRE DEL FACILITADARA:
LORENA ALONSO GUZMÁN
ALUMNO:
LAUREANO LOPEZ ALVARO FERMIN
TURNO: MATUTINO GRUPO: 401
MATRICULA : 13417747
unidad 3
sistema de ecuaciones lineales
ÍNDICE
INTRODUCCIÓN
3.1. MATRICES
3.1.1. OPERACIONES CON MATRICES
3.2. VECTORES
3.3. ELIMINACIÓN DE GAUSS
3.4. ELIMINACIÓN DE GAUSS-JORDAN
3.5. ESTRATEGIAS DE PIVOTEO
3.6. MÉTODO DE CHOLESKY
3.7. MÉTODO DE DESCOMPOSICIÓN LU
3.8. MÉTODO DE GAUSS-SEIDEL
3.9. MÉTODO ITERATIVO
3.9.1. MÉTODO JACOBI
INTRODUCCIÓN
3.1. MATRICES
3.1.1. OPERACIONES CON MATRICES
3.2. VECTORES
3.3. ELIMINACIÓN DE GAUSS
3.4. ELIMINACIÓN DE GAUSS-JORDAN
3.5. ESTRATEGIAS DE PIVOTEO
3.6. MÉTODO DE CHOLESKY
3.7. MÉTODO DE DESCOMPOSICIÓN LU
3.8. MÉTODO DE GAUSS-SEIDEL
3.9. MÉTODO ITERATIVO
3.9.1. MÉTODO JACOBI
INTRODUCCIÓN
El tema de ecuaciones lineales se basa en los ecuación que podemos obtener muchas raíz y también así variables. Tambien el análisis numérico trata de diseñar métodos para “aproximar” de una manera eficiente las soluciones de problemas expresados matemáticamente. nuestro objetivo principal es encontrar soluciones “aproximadas” a problemas complejos utilizando sólo las operaciones, se requiere de una secuencia de operaciones algebraicas y lógicas que producen, la aproximación al problema matemático.
3.1. MATRICES
En matemática, una matriz es un arreglo bidimensional de números. Dado que puede definirse tanto la suma como el producto de matrices, en mayor generalidad se dice que son elementos de un anillo. Una matriz se representa por medio de una letra mayúscula(A,B..) y sus elementos con la misma letra en minúscula (a,b...), con un doble subíndice donde el primero indica la fila y el segundo la columna a la que pertenece.
Los elementos individuales de una matriz x , a menudo denotados por y , donde el máximo valor de sus elementos (, ) en es , y el máximo valor de es . Siempre que la matriz tenga el mismo número de filas y de columnas que otra matriz, estas se pueden sumar o restar elemento por elemento.
Las matrices se utilizan para múltiples aplicaciones y sirven, en particular, para representar los coeficientes de los sistemas de ecuaciones lineales o para representar transformaciones lineales dada una base. En este último caso, las matrices desempeñan el mismo papel que los datos de un vector para las aplicaciones lineales.
Pueden sumarse, multiplicarse y descomponerse de varias formas, lo que también las hace un concepto clave en el campo del álgebra lineal.
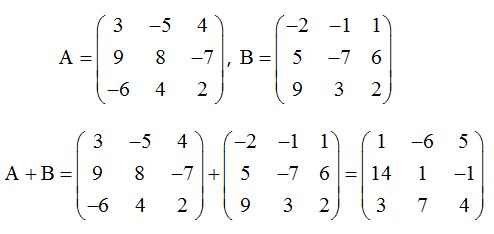
una matriz real de orden m x n siendo m y n números naturales es un conjunto de m x n números distribuidos en “m” filas y “n” columnas. Veamos los siguientes ejemplos:
Una matriz cuadrada de dos filas y 2 columnas:

Una matriz de tres filas y dos columnas:

Una matriz de 3 filas y 4 columnas:

Debemos saber que los números que componen una matriz se denominan elementos. Estos se suelen representar por la expresión aij donde “i” representa la fila y “j” la columna en la que se encuentra. Por ejemplo:


En física, un vector (también llamado vector euclidiano o vector geométrico) es una magnitud física definida en un sistema de referencia que se caracteriza por tener módulo (o longitud), dirección y orientación.
En matemáticas se define un vector como un elemento de un espacio vectorial. Esta noción es más abstracta y para muchos espacios vectoriales no es posible representar sus vectores mediante el módulo y la dirección. En particular los espacios de dimensión infinita sin producto escalar no son representables de ese modo.
Suma y resta de vectores
La suma de dos vectores libres es otro vector libre que se determina de la siguiente forma:
Se sitúa el punto de aplicación de uno de ellos sobre el extremo del otro; el vector suma es el vector que tiene su origen en el origen del primero y su extremo en el extremo del segundo.
Por tanto, el vector suma de dos vectores coincide con una de las diagonales, la "saliente", del paralelogramo que puede formarse con los vectores que se suman; la otra diagonal representa la resta de dichos vectores.

Para efectuar sumas o restas de tres o más vectores, el proceso es idéntico. Basta con aplicar la propiedad asociativa.
Al vector que se obtiene al sumar o restar varios vectores se le denomina resultante.
Suma de Vectores
La suma de los vectores podemos realizarla de dos maneras diferentes, analítica y gráficamente.
Procedimiento Gráfico
Para sumar dos vectores de manera gráfica utilizaremos la denominada Regla del paralelogramo, consistente en trasladar paralelamente los vectores hasta unirlos por el origen, y luego trazar un paralelogramo, del que obtendremos el resultado de la suma, como consecuencia de dibujar la diagonal de ese paralelogramo, como podemos ver en el siguiente dibujo:

Otra manera de expresar la suma de manera gráfica es trasladar el segundo vector a sumar de tal manera que el origen de éste, coincida con el extremo del primer vector, y la suma la obtendremos dibujando un vector que vaya desde el origen del primer vector hasta el extremo del segundo, de la siguiente manera:

Hay que tener muy presente lo siguiente: vectores en la misma dirección se suman (tal y como ya hemos visto en la sección de la suma de vectores), pero vectores con sentidos opuestos se restan (tal y como se puede ver en el apartado correspondiente a la resta de vectores). A continuación tenemos un ejemplo de suma y resta de vectores.

La diferencia entre los métodos de Gauss y de Gauss-Jordan es que el primero finaliza al obtener un sistema equivalente en forma escalonada, mientras que el segundo finaliza al obtener un sistema equivalente en forma escalonada reducida.
El método de eliminación de Gauss o simplemente método de Gauss consiste en convertir un sistema lineal de n ecuaciones con n incógnitas, en uno escalonado, en el que la primera ecuación tiene n incógnitas, la segunda ecuación tiene n - 1 incógnitas, ..., hasta la última ecuación, que tiene 1 incógnita. De esta forma, será fácil partir de la última ecuación e ir subiendo para calcular el valor de las demás incógnitas.
3.4. ELIMINACIÓN DE GAUSS-JORDAN
En matemáticas, la eliminación de Gauss, llamada así debido a Carl Friedrich Gauss y Wilhelm Jordan, es un algoritmo del álgebra lineal para determinar las soluciones de un sistema de ecuaciones lineales, encontrar matrices e inversas. Un sistema de ecuaciones se resuelve por el método de Gauss cuando se obtienen sus soluciones mediante la reducción del sistema dado a otro equivalente en el que cada ecuación tiene una incógnita menos que la anterior. El método de Gauss transforma la matriz de coeficientes en una matriz triangular superior. El método de Gauss-Jordan continúa el proceso de transformación hasta obtener una matriz diagonal.
Ejemplo
Vamos a obtener la forma escalonada reducida de la matriz ampliada
 Multiplicamos la primera fila por 1/5 y la segunda por 1/3
Multiplicamos la primera fila por 1/5 y la segunda por 1/3
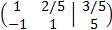
Sumamos a la segunda fila la primera
Sumamos a la segunda fila la primera
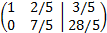 Multiplicamos la segunda fila por 5/7
Multiplicamos la segunda fila por 5/7
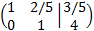
Sumamos a la primera fila la segunda fila multiplicada por -2/5
Sumamos a la primera fila la segunda fila multiplicada por -2/5
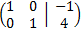
Ahora escribimos el sistema que representa esta última matriz:
Ahora escribimos el sistema que representa esta última matriz:
 Multiplicamos la primera fila por 1/5 y la segunda por 1/3
Multiplicamos la primera fila por 1/5 y la segunda por 1/3
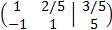
Sumamos a la segunda fila la primera
Sumamos a la segunda fila la primera
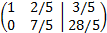 Multiplicamos la segunda fila por 5/7
Multiplicamos la segunda fila por 5/7
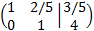
Sumamos a la primera fila la segunda fila multiplicada por -2/5
Sumamos a la primera fila la segunda fila multiplicada por -2/5
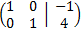
Ahora escribimos el sistema que representa esta última matriz:
Ahora escribimos el sistema que representa esta última matriz:
3.5. ESTRATEGIAS DE PIVOTEO
Cuando se aplica una operación elemental sobre una determinada fila para lograr un 0 en el coeficiente apq, con p = q + 1, q + 2, . . . ,N utilizo el elemento aqq de la matriz, y dicho elemento recibe el nombre de pivote. Los números mpq = apq/aqq se llaman multiplicadores y son los que se multiplican en la fila pivote para restarla de las correspondientes filas.
ivoteo parcial
La onda con el pivoteo es hacer Gauss-Jordan pero eligiendo el mejor valor para hacer cuentas, de manera tal que los errores de las cuentas de la maquinita sean los menores. Así, se implementa un criterio para reordenar filas de manera tal que se queden los valores mayores al momento de dividir. El método consiste en elegir en la iteración i-ésima, el elemento de la columna que sea el de mayor valor absoluto entre todos los que están por encima de la diagonal, el menor valor de p≥i
|api|=maxi≤k≤n|aki|
Pivoteo parcial escalado
Cuando hay algún valor muy zarpado en las ecuaciones en comparación con el resto, el pivoteo solito no alcanza. Ahí hay que usar escalado. El escalado implica usar un factor de escala para cada fila, que se define
sk=max1≤j≤n|akj|
ivoteo parcial
La onda con el pivoteo es hacer Gauss-Jordan pero eligiendo el mejor valor para hacer cuentas, de manera tal que los errores de las cuentas de la maquinita sean los menores. Así, se implementa un criterio para reordenar filas de manera tal que se queden los valores mayores al momento de dividir. El método consiste en elegir en la iteración i-ésima, el elemento de la columna que sea el de mayor valor absoluto entre todos los que están por encima de la diagonal, el menor valor de p≥i
|api|=maxi≤k≤n|aki|
Pivoteo parcial escalado
Cuando hay algún valor muy zarpado en las ecuaciones en comparación con el resto, el pivoteo solito no alcanza. Ahí hay que usar escalado. El escalado implica usar un factor de escala para cada fila, que se define
sk=max1≤j≤n|akj|

3.6. MÉTODO DE CHOLESKY
Cualquier matriz cuadrada A con pivotes no nulos puede ser escrita como el producto de una matriz triangular inferior L y una matriz triangular superior U; esto recibe el nombre de factorización LU. Sin embargo, si A es simétrica y definida positiva, se pueden escoger los factores tales que U es la transpuesta de L, y esto se llama la descomposición o factorización de Cholesky. Tanto la descomposición LU como la descomposición de Cholesky son usadas para resolver sistemas de ecuaciones lineales. Cuando es aplicable, la descomposición de Cholesky es dos veces más eficiente que la descomposición LU
En general, si A es Hermitiana y definida positiva, entonces A puede ser descompuesta como
donde L es una matriz triangular inferior con entradas diagonales estrictamente positivas y L* representa la conjugada traspuesta de L. Esta es la descomposición de Cholesky.
La descomposición de Cholesky es única: dada una matriz Hermitiana positiva definida A, hay una única matriz triangular inferior L con entradas diagonales estrictamente positivas tales que A = LL*. El recíproco se tiene trivialmente: si A se puede escribir como LL* para alguna matriz invertible L, triangular inferior o no, entonces A es Hermitiana y definida positiva.
El requisito de que L tenga entradas diagonales estrictamente positivas puede extenderse para el caso de la descomposición en el caso de ser semidefinida positiva. La proposición se lee ahora: una matriz cuadrada A tiene una descomposición de Cholesky si y sólo si A es Hermitiana y semidefinida positiva. Las factorizaciones de Cholesky para matrices semidefinidas positivas no son únicas en general.

Recordemos, que una matriz regulara, admite una factorización de la forma
PA=LU
Donde p es una matriz de permutación de filas, L es una matriz triangular inferior y u es una matriz triangular superior.
y sea el sistema de ecuaciones [a][x]=[b]
Aunque la eliminación gauss representa una forma satisfactoria para resolver tales sistemas, resúltate y eficiente cuando deben resolver ecuaciones con los mismos coeficientes[a], pero con diferentes constantes del lado derecho (las b).
Los métodos de descomposición LU separan el tiempo usado en las eliminaciones para la matriz [a] de las manipulaciones en el lado derecho {b}. una vez que [a] se ha “descompuesto”, los múltiples vectores del lado derecho {b} se pueden evaluar de manera eficiente.
3.8. MÉTODO DE GAUSS-SEIDEL
El método de eliminación para resolver ecuaciones simultáneas suministra soluciones suficientemente precisas hasta para 15 o 20 ecuaciones. El número exacto depende de las ecuaciones de que se trate, del número de dígitos que se conservan en el resultado de las operaciones aritméticas, y del procedimiento de redondeo. Utilizando ecuaciones de error, el número de ecuaciones que se pueden manejar se puede incrementar considerablemente a más de 15 o 20, pero este método también es impráctico cuando se presentan, por ejemplo, cientos de ecuaciones que se deben resolver simultáneamente. El método de inversión de matrices tiene limitaciones similares cuando se trabaja con números muy grandes de ecuaciones simultáneas.
Sin embargo, existen varias técnicas que se pueden utilizar, para resolver grandes números de ecuaciones simultáneas. Una de las técnicas más útiles es el método de Gauss-Seidel. Ninguno de los procedimientos alternos es totalmente satisfactorio, y el método de Gauss-Seidel tiene la desventaja de que no siempre converge a una solución o de que a veces converge muy lentamente. Sin embargo, este método convergirá siempre a una solución cuando la magnitud del coeficiente de una incógnita diferente en cada ecuación del conjunto, sea suficientemente dominante con respecto a las magnitudes de los otros coeficientes de esa ecuación.
donde:
El método de iteración Gauss-Seidel se computa, para la iteración :
donde
definimos
y
- ,
donde los coeficientes de la matriz N se definen como si , si .
Considerando el sistema con la condición de que . Entonces podemos escribir la fórmula de iteración del método
- (*)
La diferencia entre este método y el de Jacobi es que, en este último, las mejoras a las aproximaciones no se utilizan hasta completar las iteraciones.
3.9. MÉTODO ITERATIVO
Un método iterativo trata de resolver un problema matemático (como una ecuación o un sistema de ecuaciones) mediante aproximaciones sucesivas a la solución, empezando desde una estimación inicial. Esta aproximación contrasta con los métodos directos, que tratan de resolver el problema de una sola vez (como resolver un sistema de ecuaciones Ax=b encontrando la inversa de la matriz A). Los métodos iterativos son útiles para resolver problemas que involucran un número grande de variables (a veces del orden de millones), donde los métodos directos tendrían un coste prohibitivo incluso con la potencia del mejor computador disponible.
3.9.1. MÉTODO JACOBI
La base del método consiste en construir una sucesión convergente definida iterativamente. El límite de esta sucesión es precisamente la solución del sistema. A efectos prácticos si el algoritmo se detiene después de un número finito de pasos se llega a una aproximación al valor de x de la solución del sistema.
La sucesión se construye descomponiendo la matriz del sistema en la forma siguiente:
donde , es una matriz diagonal y , es la suma de una matriz triangular inferior y una matriz triangular superior , luego . Partiendo de , podemos reescribir dicha ecuación como:
Luego,
Si aii ≠ 0 para cada i. Por la regla iterativa, la definición del Método de Jacobi puede ser expresado de la forma:
donde es el contador de iteración, Finalmente tenemos:
Cabe destacar que al calcular xi(k+1) se necesitan todos los elementos en x(k), excepto el que tenga el mismo i. Por eso, al contrario que en el método Gauss-Seidel, no se puede sobreescribir xi(k) con xi(k+1), ya que su valor será necesario para el resto de los cálculos. Esta es la diferencia más significativa entre los métodos de Jacobi y Gauss-Seidel. La cantidad mínima de almacenamiento es de dos vectores de dimensión n, y será necesario realizar un copiado explícito.
BIBLIOGRAFÍA
https://www.uoc.edu/in3/emath/docs/Algebra_Matrices.pdf
https://yosoytuprofe.com/2017/06/04/operaciones-con-matrices/
https://www.ditutor.com/matrices/operciones_matrices.html
http://www.monografias.com/trabajos35/vectores/vectores.shtml
https://www.geogebra.org/m/audTn7pS



































Comentarios
Publicar un comentario